Santa Barbara's David Berenstein and his student Alexandra Miller published a paper
LLM refers to Lin, Lunin, Maldacena – it's the bubbling AdS space – and this aspect of the Berenstein-Miller paper is new. If you click at the hyperlink, you will be brought to a January 2005 blog post about LLM. The date should assure you that TRF is quite an ancient source of information about physics.
The LLM construction allows you to find a bubbling AdS-style geometry for any picture where you divide a plane to a black region and the white region. The simplest separation is two half-planes, lower and upper, but even if you make the boundary wiggly and add black bubbles to the white region or vice versa, there is still some solution.
Berenstein and Miller discuss this set of states in the \(N\to\infty\) limit of AdS/CFT. They find out that all the coherent states may be identified with trivial topologies. But they are overcomplete as a would-be basis and even states that correspond to the spacetime of a different topology may be obtained as superpositions.
While the usage of LLM is new (although I haven't quite understood why this particular example helps), the conclusion is exactly the same as one in many TRF blog posts and a paper by Raju and Papadodimas from March 2015 (the paper was one of the topics mentioned here). On Page 3, you will see an announcement
There are numerous blog posts that discuss a principle that is equivalent to it or slightly more general, the "background indifference". The principle states that in a consistent theory of quantum gravity, you may basically choose any (?) geometric background with any topology (but the right behavior at infinity, the same superselection sector), and describe the Hilbert space as excitations of that background.
For years, I haven't depended on being cited so those credit issues aren't an issue for me anymore and I am actually very happy that there are people who are reaching similar conclusions that I find more important than who gets credit for them. However, I think it's unfortunate that people like Berenstein (plus Miller), Raju, and Papadodimas who are doing really serious research in quantum gravity aren't reading papers of each other (at least in one direction). If they and others listened to me, I would be ready to produce a list of top 20 folks in this business who are obliged to read (at least quickly) all new papers by the authors from the same list. What the people who are verifiably outside my list do isn't too important.
Moreover, Raju gave a talk with this argument somewhere, referring to me and Susskind. Wasn't it actually in Santa Barbara? If it were in Santa Barbara, it's somewhat embarrassing that David has missed the talk. But maybe too many events take place in Santa Barbara that are dedicated to the overcompleteness of coherent states and why it implies that there are no state-independent operators for topology and geometry in a consistent theory of quantum gravity. ;-)
Update: No, it was Raju's talk at Strings 2014 (video, check 24:35-26:00, where Suvrat bravely and kindly insists that my blog post was nice after some laughter in the hall – just try to appreciate how many pests I would have to face even at string conferences LOL) in Princeton. Still a venue a researcher into nearly identical questions isn't supposed to overlook, I think.
Off-topic things:
I was happy to learn that Frank Wilczek's favorite word was both invented and repeatedly brought to practice in Prague. His favorite word is "defenestration". As Wikipedia mentions, defenestration defines the good Bohemian style (at least it's true for the events in 1419 and on May 23rd, 1618 (U.S. reconstruction, Czech cartoon) – we have an anniversary today) but in two hours, they may enjoy the methodology in Austria, too. ;-)
Here is the Nobel prize winner's paper (backup; soon to appear in Physical Review Letters) explaining why "defenestration" is the best word in the world.
Bizarre Twitter popularity
The most retweeted and liked tweet of mine in a long time was this piece of black humor making fun of the fact that the member of European Parliament whom I got to the office, Petr Mach, has the same surname as a schoolkid who appeared with his classmate Ms Šebestová in a famous Czech cartoon about schoolchildren with a magic telephone receiver and their puppy Jonathan. Mach, the MEP, was really sad that Adolf Born, the father of the cartoon, died yesterday. I am also sad but I haven't met Born in person, if I remember well. At any rate, I replied to Mach that my condolences go mainly to him and Ms Šebestová and people retweet it like mad.
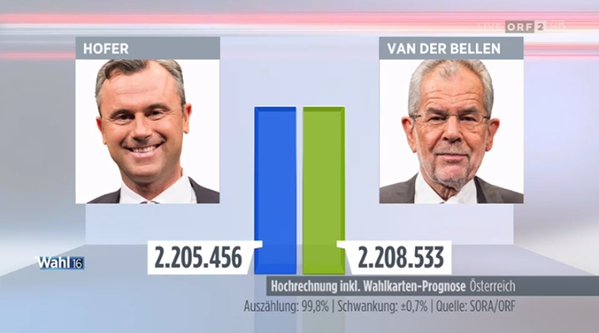
An ecoterrorist pretending to be "independent" is claimed to have beaten Norbert Hofer by 3,000 votes in Austrian presidential elections. It's not my business but I am suspicious about the bigger-than-expected difference between the the results from the regular votes (48-to-52) and the absentee ballots (60-to-40). Austrian Greens were similarly lucky (?) in 1978 when 50.47% was enough to kill their only nuclear power plant in Zwentendorf.
Topology and geometry cannot be measured by an operator measurement in quantum gravitywhich is nice because they have used the LLM limit of Maldacena's AdS/CFT correspondence to rediscover something that the TRF readers know from about 10 blog posts and that has been refined into a more controllable paper form by Papadodimas and Raju. There can't be any linear operators in a theory of quantum gravity whose eigenvalues would correspond to the topological invariants of the space. I think that the adjective "state-independent" should be added to the sentence to make it really true – Berenstein and Miller implicitly talk about state-independent operators when they talk about operators.
LLM refers to Lin, Lunin, Maldacena – it's the bubbling AdS space – and this aspect of the Berenstein-Miller paper is new. If you click at the hyperlink, you will be brought to a January 2005 blog post about LLM. The date should assure you that TRF is quite an ancient source of information about physics.
The LLM construction allows you to find a bubbling AdS-style geometry for any picture where you divide a plane to a black region and the white region. The simplest separation is two half-planes, lower and upper, but even if you make the boundary wiggly and add black bubbles to the white region or vice versa, there is still some solution.
Berenstein and Miller discuss this set of states in the \(N\to\infty\) limit of AdS/CFT. They find out that all the coherent states may be identified with trivial topologies. But they are overcomplete as a would-be basis and even states that correspond to the spacetime of a different topology may be obtained as superpositions.
While the usage of LLM is new (although I haven't quite understood why this particular example helps), the conclusion is exactly the same as one in many TRF blog posts and a paper by Raju and Papadodimas from March 2015 (the paper was one of the topics mentioned here). On Page 3, you will see an announcement
We present some evidence that it is this overcompleteness that prevents the existence of state-independent operators behind the horizon.that refers to my August 2013 argument with the same conclusion as an earlier derivation of that kind. Raju's and Papadodimas' detailed treatment of the proof is described in Appendix A which starts on Page 117. The fact that there can't be any linear operators for topology was discussed previously, e.g. in June 2013 in the context of ER=EPR.
There are numerous blog posts that discuss a principle that is equivalent to it or slightly more general, the "background indifference". The principle states that in a consistent theory of quantum gravity, you may basically choose any (?) geometric background with any topology (but the right behavior at infinity, the same superselection sector), and describe the Hilbert space as excitations of that background.
For years, I haven't depended on being cited so those credit issues aren't an issue for me anymore and I am actually very happy that there are people who are reaching similar conclusions that I find more important than who gets credit for them. However, I think it's unfortunate that people like Berenstein (plus Miller), Raju, and Papadodimas who are doing really serious research in quantum gravity aren't reading papers of each other (at least in one direction). If they and others listened to me, I would be ready to produce a list of top 20 folks in this business who are obliged to read (at least quickly) all new papers by the authors from the same list. What the people who are verifiably outside my list do isn't too important.
Moreover, Raju gave a talk with this argument somewhere, referring to me and Susskind. Wasn't it actually in Santa Barbara? If it were in Santa Barbara, it's somewhat embarrassing that David has missed the talk. But maybe too many events take place in Santa Barbara that are dedicated to the overcompleteness of coherent states and why it implies that there are no state-independent operators for topology and geometry in a consistent theory of quantum gravity. ;-)
Update: No, it was Raju's talk at Strings 2014 (video, check 24:35-26:00, where Suvrat bravely and kindly insists that my blog post was nice after some laughter in the hall – just try to appreciate how many pests I would have to face even at string conferences LOL) in Princeton. Still a venue a researcher into nearly identical questions isn't supposed to overlook, I think.
Off-topic things:
I was happy to learn that Frank Wilczek's favorite word was both invented and repeatedly brought to practice in Prague. His favorite word is "defenestration". As Wikipedia mentions, defenestration defines the good Bohemian style (at least it's true for the events in 1419 and on May 23rd, 1618 (U.S. reconstruction, Czech cartoon) – we have an anniversary today) but in two hours, they may enjoy the methodology in Austria, too. ;-)
Here is the Nobel prize winner's paper (backup; soon to appear in Physical Review Letters) explaining why "defenestration" is the best word in the world.
Bizarre Twitter popularity
The most retweeted and liked tweet of mine in a long time was this piece of black humor making fun of the fact that the member of European Parliament whom I got to the office, Petr Mach, has the same surname as a schoolkid who appeared with his classmate Ms Šebestová in a famous Czech cartoon about schoolchildren with a magic telephone receiver and their puppy Jonathan. Mach, the MEP, was really sad that Adolf Born, the father of the cartoon, died yesterday. I am also sad but I haven't met Born in person, if I remember well. At any rate, I replied to Mach that my condolences go mainly to him and Ms Šebestová and people retweet it like mad.

An ecoterrorist pretending to be "independent" is claimed to have beaten Norbert Hofer by 3,000 votes in Austrian presidential elections. It's not my business but I am suspicious about the bigger-than-expected difference between the the results from the regular votes (48-to-52) and the absentee ballots (60-to-40). Austrian Greens were similarly lucky (?) in 1978 when 50.47% was enough to kill their only nuclear power plant in Zwentendorf.
Topology, geometry in QG admit no operators, measurement
![Topology, geometry in QG admit no operators, measurement]() Reviewed by MCH
on
May 23, 2016
Rating:
Reviewed by MCH
on
May 23, 2016
Rating:



No comments: