I think that we are seeing another example of the day when the best new hep-th preprint is the first one. Although the ordering of the papers may look pointless to you and you could consider the fights to be at the top to be childish pißing contests, many authors – including some very mature and brilliant ones – are likely to place their good paper at the top because they're proud and they do some careful timing work to be at the top. To check this theory, I looked at the timing of the paper
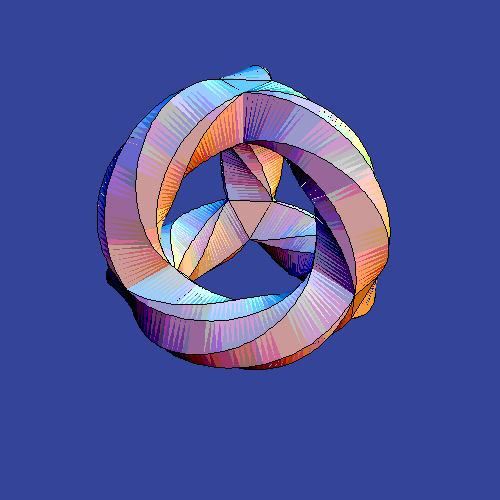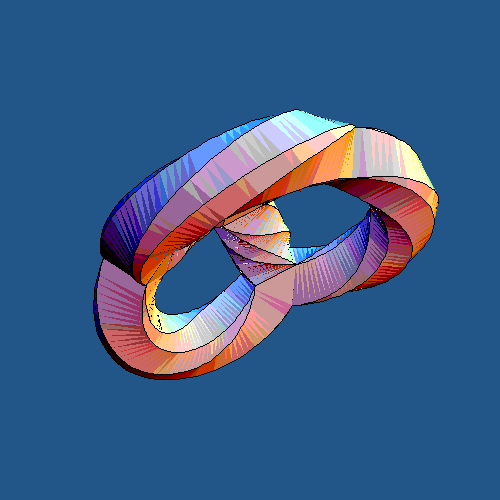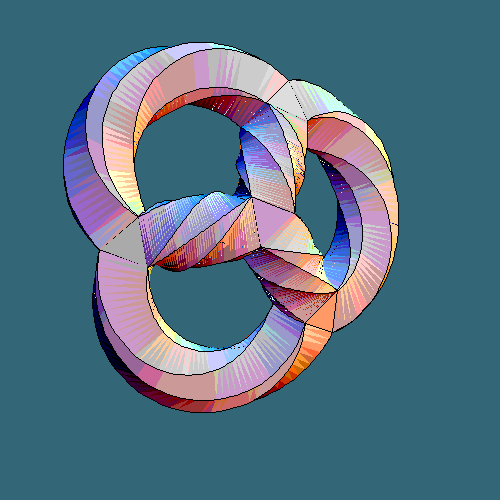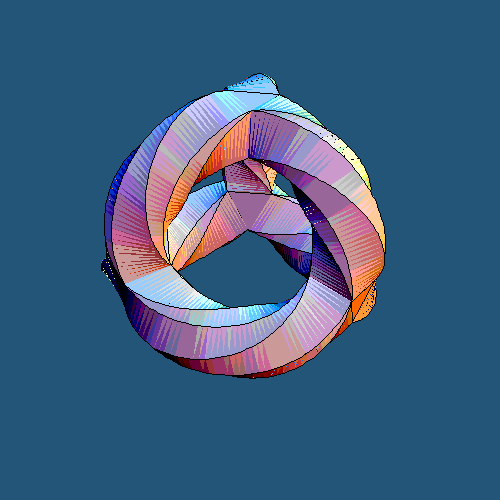
There's quite some intense competition when it comes to the timing and ordering of the papers! Should it be fought against? I actually don't think so. I think that the community benefits because the better papers' authors are really more likely to fight for the visible spots and that makes it easier for others to find the better papers.
Sadly, in one context, Shamit Kachru didn't surprise me nicely and he signed the atrocious anti-Strumia manifesto. But that hasn't prevented him from co-writing this interesting paper, either. What's going on?
Their paper is another interesting example of the string theory's power to solve seemingly intractable problems in mathematics – in this case, they have a totally new way to find the precise metrics on complicated compact manifolds. But I think that their achievement is more than that: It's a new link between algebra and geometry that basically allows the geometry of some compact manifolds to be "made out of" completely different underlying stuff.
Of course, they're not building the manifolds from LEGO or octopi, like the Smolin-style childish crackpots, but it is a clever generalized way of building the metric from some other pieces, anyway.
As you should know, string theory implies that there exist extra dimensions of space. In the vacuum, i.e. in the absence of matter sources, Einstein's equations of general relativity tell you that the Einstein's tensor vanishes. Consequently, its trace, the Ricci scalar, also vanishes, which also means that the Ricci tensor vanishes:\[
R_{\mu\nu} = 0.
\] Einstein taught us that the vacuum portions of the spacetime are Ricci-flat. Cutely enough, this condition continues to hold if the extra dimensions are added. For example, when the spacetime takes the form of the Cartesian product \(M^4 \times X\) where \(X\) is a 6-dimensional manifold, this manifold \(X\) has to be Ricci-flat, too.
So the shapes of extra dimensions aren't really arbitrary, as the anti-string crackpots love to suggest or even say. They are constrained by Einstein's equations. This constraint is even stronger for compact manifolds such as our \(X\) because aside from obeying the local differential equations at every point, the coordinates must also allow the compactness i.e. the solutions must be "periodic" in some generalized sense. This is highly nontrivial and only a finite or at most countable number of classes of solutions, each of which is described by a finite number of real parameters, obey the conditions.
When we require \(X\) to be real 4-dimensional, we only find some very special solution. Note that the four-sphere \(S^4\) is simple but it surely isn't a solution: it has positive curvature which means that it cannot be Ricci-flat. However, the four-torus \(T^4\) is a solution. Its four radia and all the angles (tilting, skewing) may be arbitrary. Are there more non-trivial Ricci-flat 4-manifolds, e.g. those that aren't Riemann-flat?
Yes, the other class is the K3 manifolds, the "simplest manifolds after the torus". They were already discovered by some 19th century mathematicians, long before string theory was born and adopted them as some of the most fundamental playgrounds. The Ricci-flatness \(R_{\mu\nu}=0\) is a set of second-order differential equations. But supersymmetry uses a trick analogous to that of the Dirac equation and turns the condition into first-order differential equations. If you find something like a "supersymmetric" manifold, it will be automatically Ricci-flat.
By the "supersymmetric" manifold, I mean a manifold whose holonomy group is \(SU(2)\), a very special subgroup of \(SO(4)\). Note that \(SO(4)\approx SU(2)\times SU(2)\) and \(SU(2)\) may be embedded in several ways into this product. Recall that the holonomy group is the group of all possible rotations – within \(O(D)\), the maximum holonomy group – that you induce by rotating a local tangent space by a round trip along any curve on which you keep the parallel transport. Generic unorientable potatoes have the \(O(D)\) holonomy, orientable potatoes have \(SO(D)\), tori have the trivial group \(\{1\}\), but there exist very important intermediate cases whose holonomy is e.g. \(U(D/2)\) or \(SU(D/2)\) or something else, e.g. \(G_2\) for \(D=7\).
The animation at the top shows some projections of sections of some K3 manifolds. The only point the animation wants to make is that they really have a rather nontrivial topology and some kind of clever beauty that you only feel after you spend a part of your life in a higher-dimensional spacetime (at least mentally).
K3 manifolds like that may be used as the shape for spacetime dimensions in very important vacua of string theory – although the phenomenologically realistic vacua require somewhat more complex, higher-dimensional cousins of the K3 manifolds – well, at least the Calabi-Yau spaces. Now: Can we pick four coordinates and write the explicit metric for such a Ricci-flat K3 manifold? We face rather nontrivial and nonlinear differential equations and the common answer was No – because no one wrote an explicit solution.
I remember very well how, in 2005, Headrick and Wiseman were presenting their numerical calculation of a K3 metric. They took a shape of the K3 that is close enough to the orbifold \(T^4/ \ZZ_2\) and tried to deform it into a non-singular K3, while describing the smooth metric by a minimum number of functions of a minimal number of variables that they could. These functions were computed numerically.
Now, they're very bright guys and they have shown that they may approach a very generic problem by some calculational techniques. But the techniques haven't really used any special, heavy tools. They were the solutions that a very bright teenager – e.g. one who likes the mathematical olympiads – could use as well, without studying much. (A paper by Donaldson discussed related numerical methods to find K3s half a year later.)
The paper by Kachru et al. is extremely different in this respect because it uses a whole army of special heavy tools – tools like string dualities that allowed them to find the K3 as a moduli space, wall-crossing formulae, Gaiotto-Moore-Neitzke and their twistor spaces for hyper-Kähler manifolds, Ooguri-Vafa and Gross-Wilson metric, instanton corrections to moduli spaces, little string theory as a non-gravitational limit of string dynamics within fivebranes, and lots of other things.
All these pieces cooperate to produce the new way to write down the (almost) explicit solution for the K3 metrics – they're elliptically fibered K3s from the quotient\[
O(18,2,\ZZ) \backslash O(18,2) / O(18) \times O(2)
\] times some additional \(\RR\) factors for scaling etc. Note that "all K3 manifolds" have \(19,3\) instead of \(18,2\), while \(20,4\) would produce K3 manifolds including allowed \(B\)-fields. The number of people in the world who have really mastered these fancy new weapons and who can combine them to derive similar results as Kachru et al. is at most comparable to twelve – and it's rather likely that the text above has already listed a majority of this set. Similar statements have been made about the difficulty of general relativity in the past but they were bogus. My statement is serious.
You know, my excitement isn't too deep when string theory helps to solve a new mathematical problem or equation – because I don't really care about isolated mathematical problems that were just randomly picked from the infinite family of possible mathematical problems. What I care about is the omnipresence of some notion of spacetime in physics – and the people's ability to look at the spacetime in entirely new ways.
The very existence of K3 manifolds – and compact Ricci-flat manifolds in general – is sort of fascinating. Why do they exist? Why does the set of such manifolds have the number of components it has, and why do those components have their dimensionalities and shapes? A priori, no crisp answers to these questions have to exist. You could believe that it is just a messy mathematical problem that has an uninspiring and messy mathematical solution – and finding it is almost guaranteed to be very close to the obvious "brute force" approach that doesn't teach you anything deep. However, string theory indicates that additional answers do exist at most times – and there is a lot of extra deep stuff waiting to be learned.
The type II string theory compactified on K3 surfaces is equivalent to heterotic string theory on four-tori. Note that the heterotic side of this "string-string duality" only involves locally flat, and therefore "trivial", spacetimes, but it knows about some highly nontrivial curved manifolds of complicated topology, the K3 surfaces. The moduli describing possible K3 surfaces may be translated to somewhat non-geometric parameters governing the propagation of the heterotic strings in a "flatter" environment. In this sense, the string-string duality trades some geometry for "non-geometry" – which is an aspect of string theory's ability to unify geometry with matter, to unify the gravitational force with all other forces.
The animation at the top is purely geometric and visually cute. But it may be translated to some algebra if not number theory, to some counting of BPS states in some appropriate stringy setup that they identified. If you generalize this observation a little bit, all nontrivial, nonlinear, curved objects that play a role in physics could be "emergent" in a similar way – or in many similar ways. And it's plausible that one of the dual perspectives on the moduli spaces could be generalized in such a way that all the equations of motion that are found anywhere in string theory are merged into one master condition, a universal definition of string/M-theory.
Such a universal definition of string/M-theory would probably obscure the very existence of geometry and smooth configuration spaces and moduli spaces to all beginners. But if you learned a package of finitely many heavy tools like Kachru et al. did, you could suddenly see all aspects of geometry and physics as some emerging pattern in the somewhat more algebraic foundations of string theory, physics, and mathematics.
K3 metrics from little string theoryby Kachru and Zimet (Stanford) and Tripathy (Harvard math) and it was submitted on Wed, 24 Oct 2018 18:00:01 UTC, i.e. one second after the point when it's guaranteed to appear today. I think that my theory has passed the test. Cutely enough, the first three or so hep-th and first three or so hep-ph papers were posted within two seconds after the critical point, too. If you want to win this game, you need to press "enter" at the right moment, within the precision of split seconds.
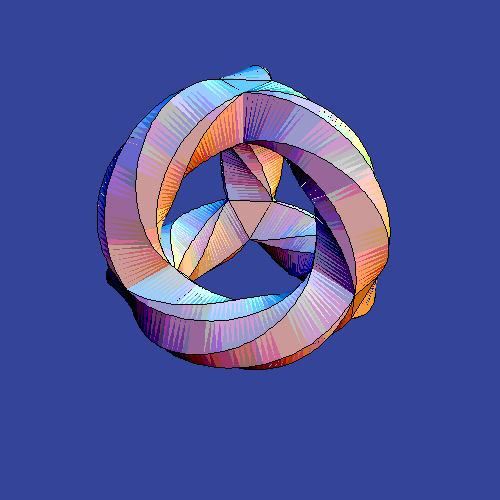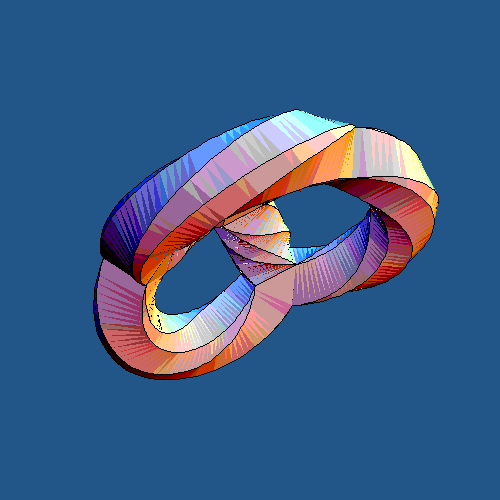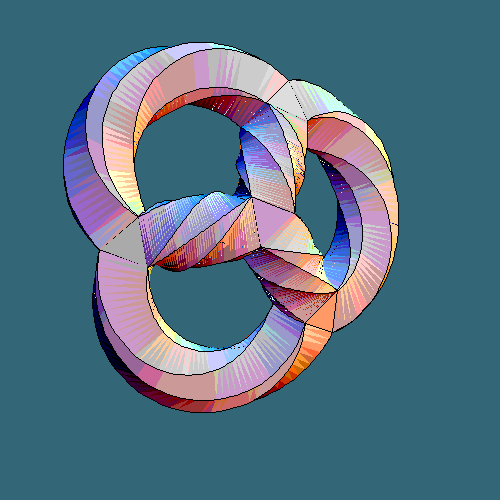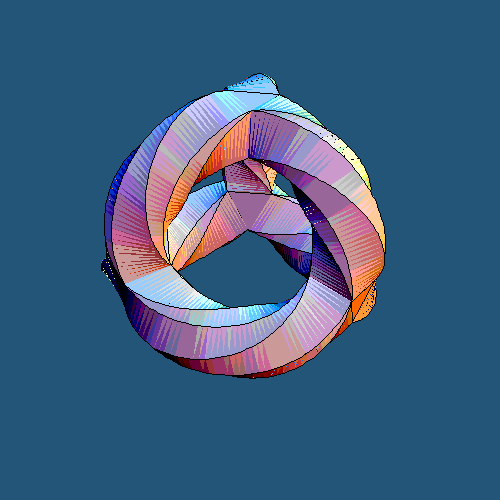
There's quite some intense competition when it comes to the timing and ordering of the papers! Should it be fought against? I actually don't think so. I think that the community benefits because the better papers' authors are really more likely to fight for the visible spots and that makes it easier for others to find the better papers.
Sadly, in one context, Shamit Kachru didn't surprise me nicely and he signed the atrocious anti-Strumia manifesto. But that hasn't prevented him from co-writing this interesting paper, either. What's going on?
Their paper is another interesting example of the string theory's power to solve seemingly intractable problems in mathematics – in this case, they have a totally new way to find the precise metrics on complicated compact manifolds. But I think that their achievement is more than that: It's a new link between algebra and geometry that basically allows the geometry of some compact manifolds to be "made out of" completely different underlying stuff.
Of course, they're not building the manifolds from LEGO or octopi, like the Smolin-style childish crackpots, but it is a clever generalized way of building the metric from some other pieces, anyway.
As you should know, string theory implies that there exist extra dimensions of space. In the vacuum, i.e. in the absence of matter sources, Einstein's equations of general relativity tell you that the Einstein's tensor vanishes. Consequently, its trace, the Ricci scalar, also vanishes, which also means that the Ricci tensor vanishes:\[
R_{\mu\nu} = 0.
\] Einstein taught us that the vacuum portions of the spacetime are Ricci-flat. Cutely enough, this condition continues to hold if the extra dimensions are added. For example, when the spacetime takes the form of the Cartesian product \(M^4 \times X\) where \(X\) is a 6-dimensional manifold, this manifold \(X\) has to be Ricci-flat, too.
So the shapes of extra dimensions aren't really arbitrary, as the anti-string crackpots love to suggest or even say. They are constrained by Einstein's equations. This constraint is even stronger for compact manifolds such as our \(X\) because aside from obeying the local differential equations at every point, the coordinates must also allow the compactness i.e. the solutions must be "periodic" in some generalized sense. This is highly nontrivial and only a finite or at most countable number of classes of solutions, each of which is described by a finite number of real parameters, obey the conditions.
When we require \(X\) to be real 4-dimensional, we only find some very special solution. Note that the four-sphere \(S^4\) is simple but it surely isn't a solution: it has positive curvature which means that it cannot be Ricci-flat. However, the four-torus \(T^4\) is a solution. Its four radia and all the angles (tilting, skewing) may be arbitrary. Are there more non-trivial Ricci-flat 4-manifolds, e.g. those that aren't Riemann-flat?
Yes, the other class is the K3 manifolds, the "simplest manifolds after the torus". They were already discovered by some 19th century mathematicians, long before string theory was born and adopted them as some of the most fundamental playgrounds. The Ricci-flatness \(R_{\mu\nu}=0\) is a set of second-order differential equations. But supersymmetry uses a trick analogous to that of the Dirac equation and turns the condition into first-order differential equations. If you find something like a "supersymmetric" manifold, it will be automatically Ricci-flat.
By the "supersymmetric" manifold, I mean a manifold whose holonomy group is \(SU(2)\), a very special subgroup of \(SO(4)\). Note that \(SO(4)\approx SU(2)\times SU(2)\) and \(SU(2)\) may be embedded in several ways into this product. Recall that the holonomy group is the group of all possible rotations – within \(O(D)\), the maximum holonomy group – that you induce by rotating a local tangent space by a round trip along any curve on which you keep the parallel transport. Generic unorientable potatoes have the \(O(D)\) holonomy, orientable potatoes have \(SO(D)\), tori have the trivial group \(\{1\}\), but there exist very important intermediate cases whose holonomy is e.g. \(U(D/2)\) or \(SU(D/2)\) or something else, e.g. \(G_2\) for \(D=7\).
The animation at the top shows some projections of sections of some K3 manifolds. The only point the animation wants to make is that they really have a rather nontrivial topology and some kind of clever beauty that you only feel after you spend a part of your life in a higher-dimensional spacetime (at least mentally).
K3 manifolds like that may be used as the shape for spacetime dimensions in very important vacua of string theory – although the phenomenologically realistic vacua require somewhat more complex, higher-dimensional cousins of the K3 manifolds – well, at least the Calabi-Yau spaces. Now: Can we pick four coordinates and write the explicit metric for such a Ricci-flat K3 manifold? We face rather nontrivial and nonlinear differential equations and the common answer was No – because no one wrote an explicit solution.
I remember very well how, in 2005, Headrick and Wiseman were presenting their numerical calculation of a K3 metric. They took a shape of the K3 that is close enough to the orbifold \(T^4/ \ZZ_2\) and tried to deform it into a non-singular K3, while describing the smooth metric by a minimum number of functions of a minimal number of variables that they could. These functions were computed numerically.
Now, they're very bright guys and they have shown that they may approach a very generic problem by some calculational techniques. But the techniques haven't really used any special, heavy tools. They were the solutions that a very bright teenager – e.g. one who likes the mathematical olympiads – could use as well, without studying much. (A paper by Donaldson discussed related numerical methods to find K3s half a year later.)
The paper by Kachru et al. is extremely different in this respect because it uses a whole army of special heavy tools – tools like string dualities that allowed them to find the K3 as a moduli space, wall-crossing formulae, Gaiotto-Moore-Neitzke and their twistor spaces for hyper-Kähler manifolds, Ooguri-Vafa and Gross-Wilson metric, instanton corrections to moduli spaces, little string theory as a non-gravitational limit of string dynamics within fivebranes, and lots of other things.
All these pieces cooperate to produce the new way to write down the (almost) explicit solution for the K3 metrics – they're elliptically fibered K3s from the quotient\[
O(18,2,\ZZ) \backslash O(18,2) / O(18) \times O(2)
\] times some additional \(\RR\) factors for scaling etc. Note that "all K3 manifolds" have \(19,3\) instead of \(18,2\), while \(20,4\) would produce K3 manifolds including allowed \(B\)-fields. The number of people in the world who have really mastered these fancy new weapons and who can combine them to derive similar results as Kachru et al. is at most comparable to twelve – and it's rather likely that the text above has already listed a majority of this set. Similar statements have been made about the difficulty of general relativity in the past but they were bogus. My statement is serious.
You know, my excitement isn't too deep when string theory helps to solve a new mathematical problem or equation – because I don't really care about isolated mathematical problems that were just randomly picked from the infinite family of possible mathematical problems. What I care about is the omnipresence of some notion of spacetime in physics – and the people's ability to look at the spacetime in entirely new ways.
The very existence of K3 manifolds – and compact Ricci-flat manifolds in general – is sort of fascinating. Why do they exist? Why does the set of such manifolds have the number of components it has, and why do those components have their dimensionalities and shapes? A priori, no crisp answers to these questions have to exist. You could believe that it is just a messy mathematical problem that has an uninspiring and messy mathematical solution – and finding it is almost guaranteed to be very close to the obvious "brute force" approach that doesn't teach you anything deep. However, string theory indicates that additional answers do exist at most times – and there is a lot of extra deep stuff waiting to be learned.
The type II string theory compactified on K3 surfaces is equivalent to heterotic string theory on four-tori. Note that the heterotic side of this "string-string duality" only involves locally flat, and therefore "trivial", spacetimes, but it knows about some highly nontrivial curved manifolds of complicated topology, the K3 surfaces. The moduli describing possible K3 surfaces may be translated to somewhat non-geometric parameters governing the propagation of the heterotic strings in a "flatter" environment. In this sense, the string-string duality trades some geometry for "non-geometry" – which is an aspect of string theory's ability to unify geometry with matter, to unify the gravitational force with all other forces.
The animation at the top is purely geometric and visually cute. But it may be translated to some algebra if not number theory, to some counting of BPS states in some appropriate stringy setup that they identified. If you generalize this observation a little bit, all nontrivial, nonlinear, curved objects that play a role in physics could be "emergent" in a similar way – or in many similar ways. And it's plausible that one of the dual perspectives on the moduli spaces could be generalized in such a way that all the equations of motion that are found anywhere in string theory are merged into one master condition, a universal definition of string/M-theory.
Such a universal definition of string/M-theory would probably obscure the very existence of geometry and smooth configuration spaces and moduli spaces to all beginners. But if you learned a package of finitely many heavy tools like Kachru et al. did, you could suddenly see all aspects of geometry and physics as some emerging pattern in the somewhat more algebraic foundations of string theory, physics, and mathematics.
K3 metrics from counting in little string theory
 Reviewed by MCH
on
October 26, 2018
Rating:
Reviewed by MCH
on
October 26, 2018
Rating:
 Reviewed by MCH
on
October 26, 2018
Rating:
Reviewed by MCH
on
October 26, 2018
Rating:




No comments: