Very unusually, Sean Carroll wrote a blog post promoting his and six co-authors' new preprint (mostly a review) about a topic that is potentially deep and that may be right – or that isn't obviously wrong.
His wife Jennifer Ouellette wrote an even better popular review for the Quanta Magazine, as Gordon pointed out.
It's about the description of spacetime as a tensor network. This theme was implicitly used in Beni Yoshida's guest blog about quantum error-correcting codes and quantum gravity five weeks ago – and in a report about a 2013 talk by Maldacena.
Here, I want to sketch what this "quantum gravity from tensor networks" stuff is and what it's not. TRF readers surely expect me to be outraged by something. The main claim that I find outrageous is Carroll's statement that in this topic
The basic picture is that you cover the spacetime by a network like this:
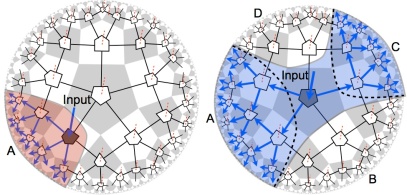
The spacetime emerges – either exactly or approximately – from such a network. Or to say the least, the network is a good toy model to understand certain features of the quantum gravitational spacetime.
That's nice but at the level of this picture, it could mean very different things.
In particular, you could say that this is nothing else than the spin network in loop quantum gravity. In that would-be theory of quantum gravity, one also imagines that the spacetime is covered by graphs like that. You could say that but it is better if you are careful about
In loop quantum gravity, one defines the wave function as a function of all the open monodromies you get on all the edges. In the tensor network approach to quantum gravity – which I will call MERA, an acronym that will be explained soon – the wave function depends on the quantum information living in the nodes, and nodes of a given "generation" in the family tree only.
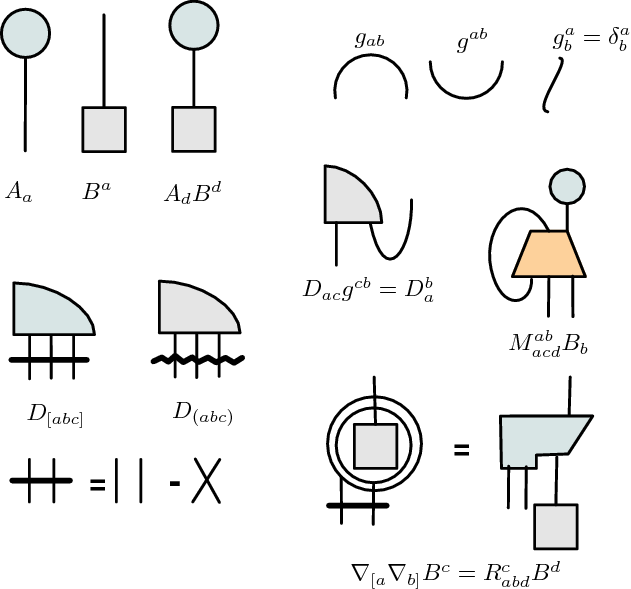
Graphs that are similar to the MERA tensor networks appear as contractions of tensors in Penrose's "multi-leg beetles" notation (see the picture above); as Feynman diagrams (see Mrs Feynman's van), and many other things. To a limited extent, MERA shares the mathematics with all of them, but the meaning of all the objects is a little bit different.
You are surely waiting for my anger so I must tell you what it is going to be about before I overwhelm you with many other historical and technical details. OK, my anger ignited by Carroll's assertion about MERA and string theory is based on two facts:
Let's look at the history of MERA, starting from 2007. Guifre Vidal began with the idea in the 2007 PRL paper
Carroll cites Evenbly and Vidal as the originators of MERA, the multi-scale entanglement renormalization Ansatz, but it was actually introduced by Vidal only in 2006. That's one of the smaller errors in Carroll's description.

What is the entanglement renormalization? It is an "improvement" of Leo Kadanoff's classic "block spins" explanation of Kenneth Wilson's renormalization group.
In the 1970s, Kadanoff realized that you may find an effective theory for many quantum degrees of freedom – all those that are living on the 4 sites in a square on the picture above – by merging these four sites into one, and replacing four by "one daddy". There was probably a reason to think that the values of the degrees of freedom on the four sites were similar, so replacing them with an average of a sort isn't too bad if you only allow "long waves". You may calculate how the "daddy squares" effectively interact with their neighbors from the interactions of the original smaller "daughter sites".
You may repeat this step many times. Merge four daddies to one granddad, and so on. In this way, you may calculate the effective theory describing ever longer distances. In the renormalization group methodology applied to quantum field theory, we usually deal with continuous changes of the length scale but the basic idea is contained in those Kadanoff's block spins, too.
At this moment, you could notice that there was nothing excessively "quantum mechanical" about Kadanoff's procedure. You may pretty much imagine that this procedure is applied to a classical theory, too. Well, in a purely classical theory, the whole power of the renormalization group would evaporate – all the renormalization group "running" is generated by the quantum processes. But conceptually, you were allowed to imagine that the degrees of freedom on the sites carried something like the "classical information".
It works for quantum theories, too. However, there is one major general phenomenon that captures what is new about quantum mechanics: entanglement. It seems that Kadanoff's game ignores entanglement between the daughters who share a daddy. But that isn't a lethal problem that makes the whole method invalid (because, in principle, all the short-distance entanglement much like the short-distance anything should become irrelevant for the long-distance questions). Instead, it is just a problem for computations. If you try to group the "spins" in a 2-dimensional (or higher-dimensional) condensed matter physics, the adjacent sites are actually entangled. This short-term entanglement accumulates too quickly and prevents you from defining the effective theory at very long distances.
Vidal's "entanglement renormalization" is a particular improvement of Kadanoff's renormalization that fights against this pernicious accumulation of entanglement. Before you merge the daughter spins into one daddy, you add one more step by Vidal: You apply disentanglers! It's some unitary transformation on the daughter spins that removes as much short-distance entanglement as you can. If you repeat these steps, "disentanglement" and "merging daughters into a daddy", many times, you may determine a better effective theory at long distances. In fact, if you look what's happening with all these disentanglers – which are effectively the vertices of the network – you may reconstruct the wave function of all the "granddaughters" in terms of a very small amount of information carried by the "great granddad".
A funny aspect analogous to the usual renormalization group is that all the RG procedures may be scale-invariant (although only under scaling factors that are discrete, e.g. powers of two or another number): in every step, you are doing the same thing and the wave function of the (scale-invariant) theory is one that entangles the granddaughters in the same way as daughters or mothers.
So Vidal's "entanglement renormalization" is a Kadanoff-style discrete renormalization group procedure with some extra step of "disentanglement" added at each layer. This step is described by some "beetles" in the network that convert some quantum information to some other quantum information. OK? MERA is an Ansatz based on the same idea.
Where is string theory in all of that? Those guys have been condensed matter physicists, weren't they? Well, they still found it a great idea to study this technique in order to understand different phases of matter, especially the topological order. Topological phases in condensed matter physics were said by Levin and Wen to occur thanks to the string net condensation.
Xiao-Gang Wen of MIT was obviously inspired by string theory. Although we came from different cultures, it was fun to interact with him. Before Christmas 2004, I invited him to the Duality Seminar at Harvard where he was talking about the string condensation, too. He tried to formulate his theories – even though they were theories in condensed matter physics – as a closed string theory of a sort. Well, I always thought and still think that what he exactly had in mind didn't satisfy all the conditions to be called "string theory" by string theorists but it was close enough. In the 1980s, Wen wrote numerous string theory papers – with co-authors such as Witten, Seiberg, and Dine.
So this methodology of constructing the ground state of a complicated system – by the repeated action of the disentanglers – was used by condensed matter physicists for a decade or so.
In 2008, Brian Swingle was a condensed matter physics graduate student at MIT and he co-wrote a paper with Wen and 2 pals about the tensor-product representations for string-net condensed states – that's actually the title. So at that time, he was already deeply incorporated into this culture of condensed matter physicists who find string theory inspiring. He was also taking John McGreevy's MIT course on string theory. Search for Swingle in these lecture notes. ;-)
But his own famous paper – his second paper – came in 2009:
To say the least, the tensor networks covering the AdS space look like a toy model of Maldacena's holographic AdS/CFT correspondence!
This toy model may have some limitations. For example, it is discrete while the AdS space is continuous. So the network may prevent you from reconstructing physics at distances shorter than (or comparable to) the AdS radius. Only at longer distances, you may get the proper holography. This comment is a major point made by the recent preprint co-authored by Carroll but you could have known it from TRF at least from Summer 2013 (search for "longer than"), too.
This point is
This construction of quantum gravitational spacetime from similar networks is therefore also closely related to the ER-EPR correspondence and Van Raamsdonk's glue-entanglement duality that he had studied for some time before that. The concept behind Swingle's toy model is great but at some point, one must ask what are the actual tensors that make a particular theory work. And one probably finds that no naive theory based on "qubits" or "qutrits" (or any finite-dimensional Hilbert space) will be quite physical.
Physical theories living in the usual continuous spacetimes almost certainly need infinite-dimensional Hilbert spaces that admit operators with continous spectra. And when one adds all these technical features, he gets another formulation of string theory – or a superselection sector of string theory. I am confident that everything that is "less than that" (less than a full-fledged string/M-theory) will either lack the local excitations or the continuous symmetries such as the local Poincaré symmetry or both. Or it will be inconsistent.
At any rate, this story shows the creative flow of ideas between high-energy theoretical physics and condensed matter theoretical physics. And when we talk about these flows that are still ongoing, "high-energy theoretical physics" really means "string theory", whether someone finds it intriguing or not (you definitely should!).
His wife Jennifer Ouellette wrote an even better popular review for the Quanta Magazine, as Gordon pointed out.
It's about the description of spacetime as a tensor network. This theme was implicitly used in Beni Yoshida's guest blog about quantum error-correcting codes and quantum gravity five weeks ago – and in a report about a 2013 talk by Maldacena.
Here, I want to sketch what this "quantum gravity from tensor networks" stuff is and what it's not. TRF readers surely expect me to be outraged by something. The main claim that I find outrageous is Carroll's statement that in this topic
"[p]erhaps more intriguingly, the idea of 'string theory' never really enters the game."Wow, quite a summary.
The basic picture is that you cover the spacetime by a network like this:

The spacetime emerges – either exactly or approximately – from such a network. Or to say the least, the network is a good toy model to understand certain features of the quantum gravitational spacetime.
That's nice but at the level of this picture, it could mean very different things.
In particular, you could say that this is nothing else than the spin network in loop quantum gravity. In that would-be theory of quantum gravity, one also imagines that the spacetime is covered by graphs like that. You could say that but it is better if you are careful about
- what you actually do with the network
- whether all nodes in the graph are equally important.
In loop quantum gravity, one defines the wave function as a function of all the open monodromies you get on all the edges. In the tensor network approach to quantum gravity – which I will call MERA, an acronym that will be explained soon – the wave function depends on the quantum information living in the nodes, and nodes of a given "generation" in the family tree only.

Graphs that are similar to the MERA tensor networks appear as contractions of tensors in Penrose's "multi-leg beetles" notation (see the picture above); as Feynman diagrams (see Mrs Feynman's van), and many other things. To a limited extent, MERA shares the mathematics with all of them, but the meaning of all the objects is a little bit different.
You are surely waiting for my anger so I must tell you what it is going to be about before I overwhelm you with many other historical and technical details. OK, my anger ignited by Carroll's assertion about MERA and string theory is based on two facts:
- pretty much at every stage, the MERA approach to quantum gravity was inspired by observations in string theory
- no fully consistent MERA model of quantum gravity that wouldn't be string theory is known (and most likely, no one is mathematically possible, either)
Let's look at the history of MERA, starting from 2007. Guifre Vidal began with the idea in the 2007 PRL paper
Entanglement renormalizationthat you may want to look at because it's rather readable and "fundamental". Early followups were written by Aguado and Vidal and Evenbly and Vidal in 2007-2008. All these people are condensed matter physicists.
Carroll cites Evenbly and Vidal as the originators of MERA, the multi-scale entanglement renormalization Ansatz, but it was actually introduced by Vidal only in 2006. That's one of the smaller errors in Carroll's description.
What is the entanglement renormalization? It is an "improvement" of Leo Kadanoff's classic "block spins" explanation of Kenneth Wilson's renormalization group.
In the 1970s, Kadanoff realized that you may find an effective theory for many quantum degrees of freedom – all those that are living on the 4 sites in a square on the picture above – by merging these four sites into one, and replacing four by "one daddy". There was probably a reason to think that the values of the degrees of freedom on the four sites were similar, so replacing them with an average of a sort isn't too bad if you only allow "long waves". You may calculate how the "daddy squares" effectively interact with their neighbors from the interactions of the original smaller "daughter sites".
You may repeat this step many times. Merge four daddies to one granddad, and so on. In this way, you may calculate the effective theory describing ever longer distances. In the renormalization group methodology applied to quantum field theory, we usually deal with continuous changes of the length scale but the basic idea is contained in those Kadanoff's block spins, too.
At this moment, you could notice that there was nothing excessively "quantum mechanical" about Kadanoff's procedure. You may pretty much imagine that this procedure is applied to a classical theory, too. Well, in a purely classical theory, the whole power of the renormalization group would evaporate – all the renormalization group "running" is generated by the quantum processes. But conceptually, you were allowed to imagine that the degrees of freedom on the sites carried something like the "classical information".
It works for quantum theories, too. However, there is one major general phenomenon that captures what is new about quantum mechanics: entanglement. It seems that Kadanoff's game ignores entanglement between the daughters who share a daddy. But that isn't a lethal problem that makes the whole method invalid (because, in principle, all the short-distance entanglement much like the short-distance anything should become irrelevant for the long-distance questions). Instead, it is just a problem for computations. If you try to group the "spins" in a 2-dimensional (or higher-dimensional) condensed matter physics, the adjacent sites are actually entangled. This short-term entanglement accumulates too quickly and prevents you from defining the effective theory at very long distances.
Vidal's "entanglement renormalization" is a particular improvement of Kadanoff's renormalization that fights against this pernicious accumulation of entanglement. Before you merge the daughter spins into one daddy, you add one more step by Vidal: You apply disentanglers! It's some unitary transformation on the daughter spins that removes as much short-distance entanglement as you can. If you repeat these steps, "disentanglement" and "merging daughters into a daddy", many times, you may determine a better effective theory at long distances. In fact, if you look what's happening with all these disentanglers – which are effectively the vertices of the network – you may reconstruct the wave function of all the "granddaughters" in terms of a very small amount of information carried by the "great granddad".
A funny aspect analogous to the usual renormalization group is that all the RG procedures may be scale-invariant (although only under scaling factors that are discrete, e.g. powers of two or another number): in every step, you are doing the same thing and the wave function of the (scale-invariant) theory is one that entangles the granddaughters in the same way as daughters or mothers.
So Vidal's "entanglement renormalization" is a Kadanoff-style discrete renormalization group procedure with some extra step of "disentanglement" added at each layer. This step is described by some "beetles" in the network that convert some quantum information to some other quantum information. OK? MERA is an Ansatz based on the same idea.
Where is string theory in all of that? Those guys have been condensed matter physicists, weren't they? Well, they still found it a great idea to study this technique in order to understand different phases of matter, especially the topological order. Topological phases in condensed matter physics were said by Levin and Wen to occur thanks to the string net condensation.
Xiao-Gang Wen of MIT was obviously inspired by string theory. Although we came from different cultures, it was fun to interact with him. Before Christmas 2004, I invited him to the Duality Seminar at Harvard where he was talking about the string condensation, too. He tried to formulate his theories – even though they were theories in condensed matter physics – as a closed string theory of a sort. Well, I always thought and still think that what he exactly had in mind didn't satisfy all the conditions to be called "string theory" by string theorists but it was close enough. In the 1980s, Wen wrote numerous string theory papers – with co-authors such as Witten, Seiberg, and Dine.
So this methodology of constructing the ground state of a complicated system – by the repeated action of the disentanglers – was used by condensed matter physicists for a decade or so.
In 2008, Brian Swingle was a condensed matter physics graduate student at MIT and he co-wrote a paper with Wen and 2 pals about the tensor-product representations for string-net condensed states – that's actually the title. So at that time, he was already deeply incorporated into this culture of condensed matter physicists who find string theory inspiring. He was also taking John McGreevy's MIT course on string theory. Search for Swingle in these lecture notes. ;-)
But his own famous paper – his second paper – came in 2009:
Entanglement Renormalization and HolographyHe said the thing that may be obvious to you by now: the MERA string networks – with the hierarchy of daughters and daddies – may be intepreted as a discretization of anti de Sitter space. And the label identifying the generation – the degree of merging the daughters – may be identified with the discretized radial (holographic) direction in the AdS/CFT correspondence.
To say the least, the tensor networks covering the AdS space look like a toy model of Maldacena's holographic AdS/CFT correspondence!
This toy model may have some limitations. For example, it is discrete while the AdS space is continuous. So the network may prevent you from reconstructing physics at distances shorter than (or comparable to) the AdS radius. Only at longer distances, you may get the proper holography. This comment is a major point made by the recent preprint co-authored by Carroll but you could have known it from TRF at least from Summer 2013 (search for "longer than"), too.
This point is
- unsurprising
- strong circumstantial evidence against Carroll's claim that you can do holography without string theory.
This construction of quantum gravitational spacetime from similar networks is therefore also closely related to the ER-EPR correspondence and Van Raamsdonk's glue-entanglement duality that he had studied for some time before that. The concept behind Swingle's toy model is great but at some point, one must ask what are the actual tensors that make a particular theory work. And one probably finds that no naive theory based on "qubits" or "qutrits" (or any finite-dimensional Hilbert space) will be quite physical.
Physical theories living in the usual continuous spacetimes almost certainly need infinite-dimensional Hilbert spaces that admit operators with continous spectra. And when one adds all these technical features, he gets another formulation of string theory – or a superselection sector of string theory. I am confident that everything that is "less than that" (less than a full-fledged string/M-theory) will either lack the local excitations or the continuous symmetries such as the local Poincaré symmetry or both. Or it will be inconsistent.
At any rate, this story shows the creative flow of ideas between high-energy theoretical physics and condensed matter theoretical physics. And when we talk about these flows that are still ongoing, "high-energy theoretical physics" really means "string theory", whether someone finds it intriguing or not (you definitely should!).
AdS/MERA, tensor networks, and string theory
![AdS/MERA, tensor networks, and string theory]() Reviewed by DAL
on
May 05, 2015
Rating:
Reviewed by DAL
on
May 05, 2015
Rating:




No comments: