Guest blog by Dr Beni Yoshida, quantum information fellow at Caltech
The lessons we learned from the Ryu-Takayanagi formula, the firewall paradox, and the ER=EPR conjecture have convinced us that quantum information theory can become a powerful tool to sharpen our understanding of various problems in high-energy physics. But many of the concepts utilized so far rely on entanglement entropy and its generalizations, quantities developed by Von Neumann more than 60 years ago. We live in the 21st century. Why don’t we use more modern concepts, such as the theory of quantum error-correcting codes?
This is certainly a challenging task because I need to make it accessible to everyone while explaining real physics behind the paper. My personal philosophy is that a toy model must be as simple as possible while capturing key properties of the system of interest. In this post, I will try to extract some key features of the AdS/CFT correspondence and construct a toy model which captures these features. This post may be a bit technical compared to other recent posts, but anyway, let me give it a try...
Bulk locality paradox and quantum error-correction
The AdS/CFT correspondence says that there is some kind of correspondence between quantum gravity on \((d+1)\)-dimensional asymptotically-AdS space and \(d\)-dimensional conformal field theory on its boundary. But how are they related?
The AdS-Rindler reconstruction tells us how to “reconstruct” a bulk operator from boundary operators. Consider a bulk operator \(\phi\) and a boundary region A on a hyperbolic space (in other words, a negatively-curved plane). On a fixed time-slice, the causal wedge of A is a bulk region enclosed by the geodesic line of A (a curve with a minimal length). The AdS-Rindler reconstruction says that \(\phi\) can be represented by some integral of local boundary operators supported on A if and only if \(\phi\) is contained inside the causal wedge of A. Of course, there are multiple regions A,B,C,… whose causal wedges contain \(\phi\), and the reconstruction should work for any such region.
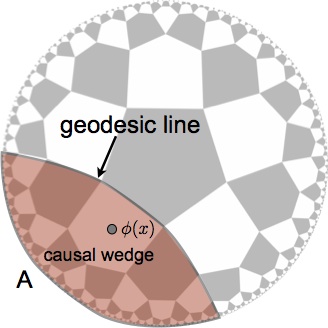
The Rindler-wedge reconstruction
That a bulk operator in the causal wedge can be reconstructed by local boundary operators, however, leads to a rather perplexing paradox in the AdS/CFT correspondence. Consider a bulk operator \(\phi\) at the center of a hyperbolic space, and split the boundary into three pieces, A, B, C. Then the geodesic line for the union of BC encloses the bulk operator, that is, \(\phi\) is contained inside the causal wedge of BC. So, \(\phi\) can be represented by local boundary operators supported on BC. But the same argument applies to AB and CA, implying that the bulk operator \(\phi\) corresponds to local boundary operators which are supported inside AB, BC, and CA simultaneously. It would seem then that the bulk operator \(\phi\) must correspond to an identity operator times a complex phase. In fact, similar arguments apply to any bulk operators, and thus, all the bulk operators must correspond to identity operators on the boundary. Then, the AdS/CFT correspondence seems so boring...
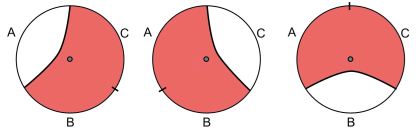
The bulk operator at the center is contained inside causal wedges of BC, AB, AC. Does this mean that the bulk operator corresponds to an identity operator on the boundary?
Almheiri, Dong, and Harlow have recently proposed an intriguing way of reconciling this paradox with the AdS/CFT correspondence [see also Polchinski et al., TRF]. They proposed that the AdS/CFT correspondence can be viewed as a quantum error-correcting code. Their idea is as follows. Instead of \(\phi\) corresponding to a single boundary operator, \(\phi\) may correspond to different operators in different regions, say \(O_{AB}\), \(O_{BC}\), \(O_{CA}\) living in AB, BC, CA respectively. Even though \(O_{AB}\), \(O_{BC}\), \(O_{CA}\) are different boundary operators, they may be equivalent inside a certain low energy subspace on the boundary.
This situation resembles the so-called quantum secret-sharing code. The quantum information at the center of the bulk cannot be accessed from any single party A, B or C because \(\phi\) does not have representation on A, B, or C. It can be accessed only if multiple parties cooperate and perform joint measurements. It seems that a quantum secret is shared among three parties, and the AdS/CFT correspondence somehow realizes the three-party quantum secret-sharing code!
Entanglement wedge reconstruction?
Recently, causal wedge reconstruction has been further generalized to the notion of entanglement wedge reconstruction. Imagine we split the boundary into four pieces A,B,C,D such that A,C are larger than B,D. Then the geodesic lines for A and C do not form the geodesic line for the union of A and C because we can draw shorter arcs by connecting endpoints of A and C, which form the global geodesic line. The entanglement wedge of AC is a bulk region enclosed by this global geodesic line of AC. And the entanglement wedge reconstruction predicts that \(\phi\) can be represented as an integral of local boundary operators on AC if and only if \(\phi\) is inside the entanglement wedge of AC [1].
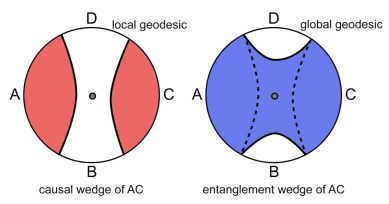
Causal wedge vs entanglement wedge.
Building a minimal toy model; the five-qubit code
Okay, now let’s try to construct a toy model which admits causal and entanglement wedge reconstructions of bulk operators. Because I want a simple toy model, I take a rather bold assumption that the bulk consists of a single qubit while the boundary consists of five qubits, denoted by A, B, C, D, E.
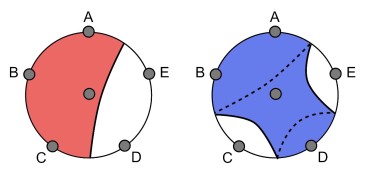
Reconstruction of a bulk operator in the “minimal” model.
What does causal wedge reconstruction teach us in this minimal setup of five and one qubits? First, we split the boundary system into two pieces, ABC and DE and observe that the bulk operator \(\phi\) is contained inside the causal wedge of ABC. From the rotational symmetries, we know that the bulk operator \(\phi\) must have representations on ABC, BCD, CDE, DEA, EAB. Next, we split the boundary system into four pieces, AB, C, D and E, and observe that the bulk operator \(\phi\) is contained inside the entanglement wedge of AB and D. So, the bulk operator \(\phi\) must have representations on ABD, BCE, CDA, DEB, EAC. In summary, we have the following:
What kinds of physical systems have such a property? Luckily, we quantum information theorists know the answer; the five-qubit code. The five-qubit code, proposed here and here, has an ability to encode one logical qubit into five-qubit entangled states and corrects any single qubit error. We can view the five-qubit code as a quantum encoding isometry from one-qubit states to five-qubit states:\[
\alpha | 0 \rangle + \beta | 1 \rangle \rightarrow \alpha | \tilde{0} \rangle + \beta | \tilde{1} \rangle
\] where \(| \tilde{0} \rangle\) and \(| \tilde{1} \rangle\) are the basis for a logical qubit. In quantum coding theory, logical Pauli operators \(\bar{X}\) and \(\bar{Z}\) are Pauli operators which act like Pauli X (bit flip) and Z (phase flip) on a logical qubit spanned by \(| \tilde{0} \rangle\) and \(| \tilde{1} \rangle\). In the five-qubit code, for any set of qubits R with volume 3, some representations of logical Pauli X and Z operators, \(\bar{X}_{R}\) and \(\bar{Z}_{R}\), can be found on R. While \(\bar{X}_{R}\) and \(\bar{X}_{R'}\) are different operators for \(R \not= R'\), they act exactly in the same manner on the codeword subspace spanned by \(| \tilde{0} \rangle\) and \(| \tilde{1} \rangle\). This is exactly the property I was looking for.
Holographic quantum error-correcting codes
We just found possibly the smallest toy model of the AdS/CFT correspondence, the five-qubit code! The remaining task is to construct a larger model. For this goal, we view the encoding isometry of the five-qubit code as a six-leg tensor. The holographic quantum code is a network of such six-leg tensors covering a hyperbolic space where each tensor has one open leg. These open legs on the bulk are interpreted as logical input legs of a quantum error-correcting code while open legs on the boundary are identified as outputs where quantum information is encoded. Then the entire tensor network can be viewed as an encoding isometry.
The six-leg tensor has some nice properties. Imagine we inject some Pauli operator into one of six legs in the tensor. Then, for any given choice of three legs, there always exists a Pauli operator acting on them which counteracts the effect of the injection. An example is shown below:
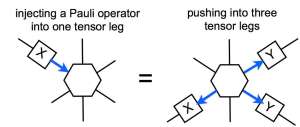
In other words, if an operator is injected from one tensor leg, one can “push” it into other three tensor legs.
Finally, let’s demonstrate causal wedge reconstruction of bulk logical operators. Pick an arbitrary open tensor leg in the bulk and inject some Pauli operator into it. We can “push” it into three tensor legs, which are then injected into neighboring tensors. By repeatedly pushing operators to the boundary in the network, we eventually have some representation of the operator living on a piece of boundary region A. And the bulk operator is contained inside the causal wedge of A. (Here, the length of the curve can be defined as the number of tensor legs cut by the curve). You can also push operators into the boundary by choosing different tensor legs which lead to different representations of a logical operator. You can even have a rather exotic representation which is supported non-locally over two disjoint pieces of the boundary, realizing entanglement wedge reconstruction.
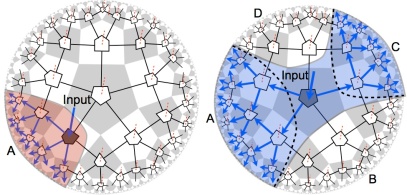
Causal wedge and entanglement wedge reconstruction.
What’s next?
This post is already pretty long and I need to wrap it up…
Shor’s quantum factoring algorithm is a revolutionary invention which opened a whole new research avenue of quantum information science. It is often forgotten, but the first quantum error-correcting code is another important invention by Peter Shor (and independently by Andrew Steane) which enabled a proof that the quantum computation can be performed fault-tolerantly. The theory of quantum error-correcting codes has found interesting applications in studies of condensed matter physics, such as topological phases of matter. Perhaps then, quantum coding theory will also find applications in high energy physics.
Indeed, many interesting open problems are awaiting us. Is entanglement wedge reconstruction a generic feature of tensor networks? How do we describe black holes by quantum error-correcting codes? Can we build a fast scrambler by tensor networks? Is entanglement a wormhole (or maybe a perfect tensor)? Can we resolve the firewall paradox by holographic quantum codes? Can the physics of quantum gravity be described by tensor networks? Or can the theory of quantum gravity provide us with novel constructions of quantum codes?
I feel that now is the time for quantum information scientists to jump into the research of black holes. We don’t know if we will be burned by a firewall or not..., but it is worth trying.
1. Whether entanglement wedge reconstruction is possible in the AdS/CFT correspondence or not still remains controversial. In the spirit of the Ryu-Takayanagi formula which relates entanglement entropy to the length of a global geodesic line, entanglement wedge reconstruction seems natural. But that a bulk operator can be reconstructed from boundary operators on two separate pieces A and C non-locally sounds rather exotic. In our paper, we constructed a toy model of tensor networks which allows both causal and entanglement wedge reconstruction in many cases. For details, see our paper.
The lessons we learned from the Ryu-Takayanagi formula, the firewall paradox, and the ER=EPR conjecture have convinced us that quantum information theory can become a powerful tool to sharpen our understanding of various problems in high-energy physics. But many of the concepts utilized so far rely on entanglement entropy and its generalizations, quantities developed by Von Neumann more than 60 years ago. We live in the 21st century. Why don’t we use more modern concepts, such as the theory of quantum error-correcting codes?Off-topic, LHC: CERN sent quite some current to the shorted segment of the circuit, apparently melted and destroyed the offending metallic piece in a diode box, and miraculously cured the LHC! Restart could be within days. LMIn a recent paper with Daniel Harlow, Fernando Pastawski and John Preskill, we have proposed a toy model of the AdS/CFT correspondence based on quantum error-correcting codes. Fernando has already written how this research project started after a fateful visit by Daniel to Caltech and John’s remarkable prediction in 1999. In this post, I hope to write an introduction which may serve as a reader’s guide to our paper, explaining why I’m so fascinated by the beauty of the toy model.
This is certainly a challenging task because I need to make it accessible to everyone while explaining real physics behind the paper. My personal philosophy is that a toy model must be as simple as possible while capturing key properties of the system of interest. In this post, I will try to extract some key features of the AdS/CFT correspondence and construct a toy model which captures these features. This post may be a bit technical compared to other recent posts, but anyway, let me give it a try...
Bulk locality paradox and quantum error-correction
The AdS/CFT correspondence says that there is some kind of correspondence between quantum gravity on \((d+1)\)-dimensional asymptotically-AdS space and \(d\)-dimensional conformal field theory on its boundary. But how are they related?
The AdS-Rindler reconstruction tells us how to “reconstruct” a bulk operator from boundary operators. Consider a bulk operator \(\phi\) and a boundary region A on a hyperbolic space (in other words, a negatively-curved plane). On a fixed time-slice, the causal wedge of A is a bulk region enclosed by the geodesic line of A (a curve with a minimal length). The AdS-Rindler reconstruction says that \(\phi\) can be represented by some integral of local boundary operators supported on A if and only if \(\phi\) is contained inside the causal wedge of A. Of course, there are multiple regions A,B,C,… whose causal wedges contain \(\phi\), and the reconstruction should work for any such region.
The Rindler-wedge reconstruction
That a bulk operator in the causal wedge can be reconstructed by local boundary operators, however, leads to a rather perplexing paradox in the AdS/CFT correspondence. Consider a bulk operator \(\phi\) at the center of a hyperbolic space, and split the boundary into three pieces, A, B, C. Then the geodesic line for the union of BC encloses the bulk operator, that is, \(\phi\) is contained inside the causal wedge of BC. So, \(\phi\) can be represented by local boundary operators supported on BC. But the same argument applies to AB and CA, implying that the bulk operator \(\phi\) corresponds to local boundary operators which are supported inside AB, BC, and CA simultaneously. It would seem then that the bulk operator \(\phi\) must correspond to an identity operator times a complex phase. In fact, similar arguments apply to any bulk operators, and thus, all the bulk operators must correspond to identity operators on the boundary. Then, the AdS/CFT correspondence seems so boring...
The bulk operator at the center is contained inside causal wedges of BC, AB, AC. Does this mean that the bulk operator corresponds to an identity operator on the boundary?
Almheiri, Dong, and Harlow have recently proposed an intriguing way of reconciling this paradox with the AdS/CFT correspondence [see also Polchinski et al., TRF]. They proposed that the AdS/CFT correspondence can be viewed as a quantum error-correcting code. Their idea is as follows. Instead of \(\phi\) corresponding to a single boundary operator, \(\phi\) may correspond to different operators in different regions, say \(O_{AB}\), \(O_{BC}\), \(O_{CA}\) living in AB, BC, CA respectively. Even though \(O_{AB}\), \(O_{BC}\), \(O_{CA}\) are different boundary operators, they may be equivalent inside a certain low energy subspace on the boundary.
This situation resembles the so-called quantum secret-sharing code. The quantum information at the center of the bulk cannot be accessed from any single party A, B or C because \(\phi\) does not have representation on A, B, or C. It can be accessed only if multiple parties cooperate and perform joint measurements. It seems that a quantum secret is shared among three parties, and the AdS/CFT correspondence somehow realizes the three-party quantum secret-sharing code!
Entanglement wedge reconstruction?
Recently, causal wedge reconstruction has been further generalized to the notion of entanglement wedge reconstruction. Imagine we split the boundary into four pieces A,B,C,D such that A,C are larger than B,D. Then the geodesic lines for A and C do not form the geodesic line for the union of A and C because we can draw shorter arcs by connecting endpoints of A and C, which form the global geodesic line. The entanglement wedge of AC is a bulk region enclosed by this global geodesic line of AC. And the entanglement wedge reconstruction predicts that \(\phi\) can be represented as an integral of local boundary operators on AC if and only if \(\phi\) is inside the entanglement wedge of AC [1].
Causal wedge vs entanglement wedge.
Building a minimal toy model; the five-qubit code
Okay, now let’s try to construct a toy model which admits causal and entanglement wedge reconstructions of bulk operators. Because I want a simple toy model, I take a rather bold assumption that the bulk consists of a single qubit while the boundary consists of five qubits, denoted by A, B, C, D, E.
Reconstruction of a bulk operator in the “minimal” model.
What does causal wedge reconstruction teach us in this minimal setup of five and one qubits? First, we split the boundary system into two pieces, ABC and DE and observe that the bulk operator \(\phi\) is contained inside the causal wedge of ABC. From the rotational symmetries, we know that the bulk operator \(\phi\) must have representations on ABC, BCD, CDE, DEA, EAB. Next, we split the boundary system into four pieces, AB, C, D and E, and observe that the bulk operator \(\phi\) is contained inside the entanglement wedge of AB and D. So, the bulk operator \(\phi\) must have representations on ABD, BCE, CDA, DEB, EAC. In summary, we have the following:
The bulk operator must have representations on R if and only if R contains three or more qubits.This is the property I want my toy model to possess.
What kinds of physical systems have such a property? Luckily, we quantum information theorists know the answer; the five-qubit code. The five-qubit code, proposed here and here, has an ability to encode one logical qubit into five-qubit entangled states and corrects any single qubit error. We can view the five-qubit code as a quantum encoding isometry from one-qubit states to five-qubit states:\[
\alpha | 0 \rangle + \beta | 1 \rangle \rightarrow \alpha | \tilde{0} \rangle + \beta | \tilde{1} \rangle
\] where \(| \tilde{0} \rangle\) and \(| \tilde{1} \rangle\) are the basis for a logical qubit. In quantum coding theory, logical Pauli operators \(\bar{X}\) and \(\bar{Z}\) are Pauli operators which act like Pauli X (bit flip) and Z (phase flip) on a logical qubit spanned by \(| \tilde{0} \rangle\) and \(| \tilde{1} \rangle\). In the five-qubit code, for any set of qubits R with volume 3, some representations of logical Pauli X and Z operators, \(\bar{X}_{R}\) and \(\bar{Z}_{R}\), can be found on R. While \(\bar{X}_{R}\) and \(\bar{X}_{R'}\) are different operators for \(R \not= R'\), they act exactly in the same manner on the codeword subspace spanned by \(| \tilde{0} \rangle\) and \(| \tilde{1} \rangle\). This is exactly the property I was looking for.
Holographic quantum error-correcting codes
We just found possibly the smallest toy model of the AdS/CFT correspondence, the five-qubit code! The remaining task is to construct a larger model. For this goal, we view the encoding isometry of the five-qubit code as a six-leg tensor. The holographic quantum code is a network of such six-leg tensors covering a hyperbolic space where each tensor has one open leg. These open legs on the bulk are interpreted as logical input legs of a quantum error-correcting code while open legs on the boundary are identified as outputs where quantum information is encoded. Then the entire tensor network can be viewed as an encoding isometry.
The six-leg tensor has some nice properties. Imagine we inject some Pauli operator into one of six legs in the tensor. Then, for any given choice of three legs, there always exists a Pauli operator acting on them which counteracts the effect of the injection. An example is shown below:
In other words, if an operator is injected from one tensor leg, one can “push” it into other three tensor legs.
Finally, let’s demonstrate causal wedge reconstruction of bulk logical operators. Pick an arbitrary open tensor leg in the bulk and inject some Pauli operator into it. We can “push” it into three tensor legs, which are then injected into neighboring tensors. By repeatedly pushing operators to the boundary in the network, we eventually have some representation of the operator living on a piece of boundary region A. And the bulk operator is contained inside the causal wedge of A. (Here, the length of the curve can be defined as the number of tensor legs cut by the curve). You can also push operators into the boundary by choosing different tensor legs which lead to different representations of a logical operator. You can even have a rather exotic representation which is supported non-locally over two disjoint pieces of the boundary, realizing entanglement wedge reconstruction.
Causal wedge and entanglement wedge reconstruction.
What’s next?
This post is already pretty long and I need to wrap it up…
Shor’s quantum factoring algorithm is a revolutionary invention which opened a whole new research avenue of quantum information science. It is often forgotten, but the first quantum error-correcting code is another important invention by Peter Shor (and independently by Andrew Steane) which enabled a proof that the quantum computation can be performed fault-tolerantly. The theory of quantum error-correcting codes has found interesting applications in studies of condensed matter physics, such as topological phases of matter. Perhaps then, quantum coding theory will also find applications in high energy physics.
Indeed, many interesting open problems are awaiting us. Is entanglement wedge reconstruction a generic feature of tensor networks? How do we describe black holes by quantum error-correcting codes? Can we build a fast scrambler by tensor networks? Is entanglement a wormhole (or maybe a perfect tensor)? Can we resolve the firewall paradox by holographic quantum codes? Can the physics of quantum gravity be described by tensor networks? Or can the theory of quantum gravity provide us with novel constructions of quantum codes?
I feel that now is the time for quantum information scientists to jump into the research of black holes. We don’t know if we will be burned by a firewall or not..., but it is worth trying.
1. Whether entanglement wedge reconstruction is possible in the AdS/CFT correspondence or not still remains controversial. In the spirit of the Ryu-Takayanagi formula which relates entanglement entropy to the length of a global geodesic line, entanglement wedge reconstruction seems natural. But that a bulk operator can be reconstructed from boundary operators on two separate pieces A and C non-locally sounds rather exotic. In our paper, we constructed a toy model of tensor networks which allows both causal and entanglement wedge reconstruction in many cases. For details, see our paper.
Quantum gravity from quantum error-correcting codes?
![Quantum gravity from quantum error-correcting codes?]()
Reviewed by DAL
on
March 30, 2015
Rating:
No comments: