...and also Baron Loránd Eötvös...
This CV looks ordinary but it is an experiment. ;-)
John Dalton was born to a family of a weaver (and Quakers, independent Christians dissatisfied with the existing denominations) in Northwest England on September 6th, 1766.
He died on July 27th, 1844 i.e. 169 years ago.
He is known for insights on color blindness (Daltonism), atomic theory (that we will discuss in detail), chemistry, and meteorology (the Dalton minimum of solar activity is named after him, too). He also wrote a book on English grammar in 1801. ;-)
He died in 1844 after his third stroke.
As a kid, he was already helping his brother to run a Quaker school. Elihu Robinson, a competent Quaker experimental weather scientist, inspired John to study the weather. Dalton did quite a lot of original work in meteorology that was mostly ignored. Later, John Gough, a blind philosopher and polymath, also taught John Dalton a lot of other science and helped him to become a teacher of maths and natural sciences in Manchester.
Color blindness
He was actually the first man who scientifically talked about color blindness in 1794, in his paper for the Manchester "Lit & Phil" (not to be confused with Lit Crit!) society. It was a pioneering contribution but his theory was wrong, as he learned in his lifetime. He thought that the eyeball liquid was discolored in color-blind people.
His own eyeball was preserved and it turned out that he had a rare type of color blindness in which the "green" (medium wavelength) cones are completely missing. Imagine that you see #RR00BB instead of #RRGGBB in the red-green-blue notation. This disorder is called deuteroanopia: see his "rainbow". In most cases of color blindness, these "green" cones are not quite missing but they have a mutated pigment.
I won't talk about the Dalton minimum and sunspots here because the climate is not supposed to be the main focus of this text. Instead, let us look at:
Atomic theory
First, in 1800 when he became a secretary of the "Lit & Phil" society, he began to study pressure of liquids and gases. A few years before the official discoveries, he verbally (and vaguely) formulated Gay-Lussac's and/or Charles's law about the expansion of liquids.
In 1801, he stated his Dalton's law: partial pressures of individual gases should be added to get the total result. Note that this law, one that can be given experimental evidence, strongly suggests that the different gases may "overlap" i.e. they should occupy different parts of the volume. That is already a strong hint of the atomic theory.
More importantly, he formulated the law of multiple proportions: when chemical elements combine, the ratios of their "amounts" are given by rational numbers with small numerators and denominators. We have CO and CO2 but not CO1.8. The "amounts" must be measured in moles: however, the actual term "mole" was only introduced in 1893, almost a century later.
For each compound, one mole corresponds to a different mass so we must choose different units in which the "amounts" are integer-valued. (But if you evaporate them, one "mole" always corresponds to the same volume under the same pressure and temperature. I don't quite understand whether Dalton was aware of this correct normalization: probably not.)
At any rate, in some proper units, the mixing ratios are rational. This strongly suggests a discrete underlying structure: atoms. He was not the first one to talk about this concept: Democritus and Lucretius did it millenia ago. But Dalton's picture was somewhat more modern. He also introduced a terminology for molecules that wasn't quite modern: the compounds with 2,3,4 atoms were called binary, ternary, quaternary compounds: see his picture of a new system of chemical philosophy.
He understood the following points properly:
Of course, Dalton neglected nuclear physics in his principles: atoms of the same element may differ by the number of neutrons (isotopes) and other reactions, nuclear reactions, can also change the identity of the atoms. But we shouldn't ask for too much from a thinker in 1800.
Testability
I want to add some comments about the testability of ideas and the time-dependence of the amount and character of evidence in favor of the atomic theory. In the ancient Greece, comments about atoms were pure philosophy that was scientifically as good (or bad) as other conceivable philosophies.
But during Dalton's life, things were already very different. The law of partial pressures and especially the rational mixing ratios were extremely powerful weapons that could falsify or at least strongly disfavor many specific enough models that contradicted the existence of atoms. These laws surely didn't tell us everything we wanted to know about the structure of matter: however, they certainly told us something - a lot, in fact - and only scientific dilletantes could think otherwise.
Once the moles were introduced, people could verify new consistency checks about the atoms. Finally, the scientific enemies of the atoms evaporated in 1905 when Einstein correctly explained the Brownian motion (in work also independently pursued by Marian Smoluchowski in 1906). The alternative theories that would explain the chaotic motion of particles in liquids had to be extremely contrived, especially if they wanted to achieve the "distance goes like square root of time" power law for the random walk.
It had to be a random walk and its typical constants were pretty much universal so they had to prove some discrete collisions of basic and rather universal building blocks of all materials: the atoms and molecules. The coefficients told us something about the size of the atoms, too. All these things occurred long before we could actually "see" atoms just a few decades ago. The people who say that they must first see quarks or strings before they take the theory seriously don't tell us anything valuable about science: the only thing these people reveal is that they're narrow-minded, uncreative, slow idiots.
Baron Loránd Eötvös de Vásárosnamény: 165th birthday
Baron Loránd von Eötvös was born in Buda into an aristocratic family connected with Vásárosnamény, Hungary - a town near Ukraine - 165 years ago, on July 27th, 1848.
Fortunately, Lóránd wrote both in Hungarian and German which is why most of the world can learn about his results (and forget about his full Hungarian name, Vásárosnaményi Báro Eötvös Lóránd). He focused on surface tension of liquids and gravity.
His father József was a statesman, educator, and novelist who was also a friend with Franz Liszt, the composer. When Lóránd was born, his father was a minister in the 1848 revolutionary government for a while. Gusztáv Keleti, a painter, was chosen as Lóránd's tutor, and the young future physicist turned out to be real good in drawing (especially on his trips) and poetry. Later, he became one of Europe's best mountaineers (and took a lot of photographs on his trips). He has also climbed a few peaks in the Dolomites so that one of them (in the middle of the picture below) is even named after him!
He wasn't bad. But let's return to his youth.
He studied many subjects at school. His interest in maths and physics clashed with the family tradition. So he entered the University of Pest in 1865 to study the law and become a politician. (The city was merged with Buda into Budapest in 1872.) Lóránd was taking private math lessons from Otto Petzval. His father accepted that it was science, not the law, that his son should pursue.
Lóránd worked in a chemistry lab before he moved to Heidelberg in 1867 (under Kirchhoff who taught him to make accurate measurements and Helmholtz who showed him the power of personal discussions - and others) where police cautioned him just because he was loudly singing on the street with his friends! :-)
Incidentally, the current students of the Eötvös Loránd University clearly follow his example.
After some time in Königsberg (where Franz Neumann taught him a lot about potentials and theoretical physics in general), he received a PhD in Heidelberg in 1870 (the thesis was about Fizeau's problems, one of the early steps that helped special relativity).
Once his dad died in 1871, he returned to Hungary and inherited the dad's title and a chair in the upper house of the Hungarian Parliament in 1872. In politics, he would later do some things related to education and research - for example, he founded the Mathematical and Physical Society, later named after him. But let's return to 1871. Lóránd instantly became a privatdozent of theoretical physics and added experimental physics a few years later. He married Gizella Horváth, a politician's daughter and a skillful pianist with a cool handwriting who spoke French well. Their daughters - see/click the picture on the left - became celebrities as athletes.
He returned to the problem of surface tension (from his student years in Königsberg) in 1876 and spent a decade with it. He measured it accurately and showed that its temperature dependence is universal for all liquids (Eötvös rule):\[
{\rm SurfaceTension} \times {\rm MolarVolume}^{2/3} =\\
= {\rm EötvösConst} \times ({\rm TemperatureCritical} - {\rm Temperature})
\] In 1886, he fully focused on gravity which was his big scientific topic until the end of his life in 1919. And of course, he is most famous for his experiments that I will discuss in the rest of this text:
Torsion balance experiments
How did he begin to study this problem? Well, the University of Göttingen offered a prize for someone who would improve the experiments initiated by Galileo that show that the acceleration in the gravitational field is universal for all materials. And Lóránd was the right one to recycle and update the design of Henry Cavendish's experiment from the late 18th century and to improve the accuracy behind the weak equivalence principle to 5 parts per billion, much better than what Newton and Bessel have achieved previously.
In the Eötvös experiment, two different masses are attached to the ends of a horizontal rod, hung from a thin string. The rotation of the rod is monitored by looking at a mirror attached to the rod (or string) through a telescope.
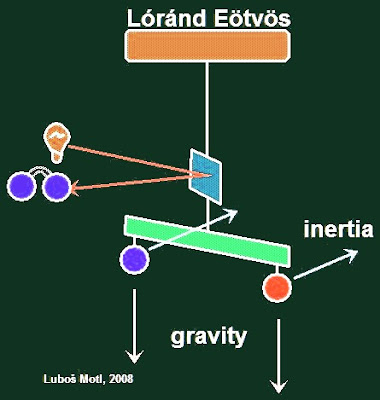
If the inertial and gravitational masses were different, the Earth's gravitational acceleration (proportional to the gravitational masses) would act on the masses differently than the centrifugal "radius times omega squared" force from the Earth's spin (proportional to the inertial masses). I assume that I can afford a simple jargon because you know how to calculate these things and I don't have to introduce more accurate concepts such as the "centripetal force". This mismatch would make the rod rotate which could be seen pretty well through the telescope.
Of course no mismatch of this sort has ever been measured - even though the experimenters in the 21st century such as those in the Eot-Wash group in the Washington state are almost 1 million times more accurate than their old Hungarian colleagues.
Consequences
The weak equivalence principle demonstrated by this experiment is, of course, one of the key principles behind the general theory of relativity. General relativity satisfies this principle: it was, in fact, historically constructed by Einstein who assumed this principle once he appreciated its strength. Newton's theory agreed with this principle by choice. However, unlike general relativity, it didn't explain the principle because one could have written down a similar theory where the masses are different.
This old-fashioned, classical principle is a huge problem for all speculative physicists who try to invent a theory of "emergent" gravity where the gravitational force results from something else than the curvature of space and time - such as new kinds of superconductivity. If you can't find a reason why the description of gravity at long distances in your theory is going to be exactly equivalent to the curved spacetime as envisioned by general relativity, it is pretty much guaranteed that your theory doesn't satisfy the principle exactly.
The probability that your theory satisfies the principle approximately and it is compatible with the experimental bounds on the violation of the principle is equal to \(10^{-16}\) or less, a number related to the accuracy of the experimental tests of the equivalence principle. If there's no good reason for the double ratio of inertial and gravitational masses of protons and neutrons to be equal to one, a generic theory is going to predict this double ratio to be a "random number different from one". And the probability that such a random number differs from one by less than \(10^{-16}\) is comparable to \(10^{-16}\). Different materials, with different proportions of protons and neutrons, will respond differently and twist the torsion gadget.
In other words, people like Robert Laughlin are pretty much screwed.
How does it work in string theory? In perturbative string theory, you may derive gravity through the interactions caused by the exchange of gravitons which are closed strings in a particular vibrational state. At the beginning, you don't see any equivalence principle over here and you might be afraid that string theory is going to follow the fate of Laughlin's or Smolin's theories of gravity and go glub, glub, glub to the bottom of the sea before they even get a chance to put them out there. ;-)
However, when you study the theory more carefully, you will be able to prove that the presence of an additional graviton - a particular closed string - in any particular scattering process has an indistinguishable physical impact from a modification of the background geometry where all the strings propagate: see
At any rate, the equivalence principle is exactly satisfied by string theory even though some descriptions of string theory are able to obscure the reasons and make the principle look like a miracle to a physicist who hasn't studied physics of the theory intensely enough. But if the reasons behind a feature of a theory are obscured, it is just the theorist's potential problem or a complication: it is not a problem of the theory itself. What matters for the fate of a theory is whether its propositions are true, as checked by observations, not whether they are easy to see. And for string theory, it is the case: its predictions related to the equivalence principle are right.
Matrix theory and AdS/CFT obscure the reasons, too. These two approaches don't even allow you to start with a general curved background, at least not in a simple way. Also, you can see the physical polarizations of the gravitons only: the pure gauge polarizations are absent from scratch. However, one can still prove that all the general facts about gravity that normally follow from general relativity are exactly satisfied because these theories - e.g. Matrix theory and AdS/CFT - can be shown to be exactly equivalent to other descriptions where the equivalence principle is manifest.
So if a theory has any chance to describe gravity as we know it today, the metric tensor must be demonstrably present in its low-energy limit and it must be possible to see that other kinds of matter depend on this metric tensor in the same way as they depend in general relativity. Because the metric tensor without anything else can't lead to finite amplitudes at higher energies, we also need some additional players in the story.
The physical phenomena and backgrounds connected in the rich network that we continue to call string theory are the only mathematically possible quantum solutions to the combined problem of finiteness and equivalence principle. It's the only framework where the curved geometry is sufficiently emergent to tame the infinities and to tell us about the inner nature of the force but also sufficiently manifest to agree with the equivalence principle as tested by the experiments initiated by this Hungarian nobleman.
And that's the memo.
This CV looks ordinary but it is an experiment. ;-)John Dalton was born to a family of a weaver (and Quakers, independent Christians dissatisfied with the existing denominations) in Northwest England on September 6th, 1766.
He died on July 27th, 1844 i.e. 169 years ago.
He is known for insights on color blindness (Daltonism), atomic theory (that we will discuss in detail), chemistry, and meteorology (the Dalton minimum of solar activity is named after him, too). He also wrote a book on English grammar in 1801. ;-)
He died in 1844 after his third stroke.
As a kid, he was already helping his brother to run a Quaker school. Elihu Robinson, a competent Quaker experimental weather scientist, inspired John to study the weather. Dalton did quite a lot of original work in meteorology that was mostly ignored. Later, John Gough, a blind philosopher and polymath, also taught John Dalton a lot of other science and helped him to become a teacher of maths and natural sciences in Manchester.
Color blindness
He was actually the first man who scientifically talked about color blindness in 1794, in his paper for the Manchester "Lit & Phil" (not to be confused with Lit Crit!) society. It was a pioneering contribution but his theory was wrong, as he learned in his lifetime. He thought that the eyeball liquid was discolored in color-blind people.
His own eyeball was preserved and it turned out that he had a rare type of color blindness in which the "green" (medium wavelength) cones are completely missing. Imagine that you see #RR00BB instead of #RRGGBB in the red-green-blue notation. This disorder is called deuteroanopia: see his "rainbow". In most cases of color blindness, these "green" cones are not quite missing but they have a mutated pigment.
I won't talk about the Dalton minimum and sunspots here because the climate is not supposed to be the main focus of this text. Instead, let us look at:
Atomic theory
First, in 1800 when he became a secretary of the "Lit & Phil" society, he began to study pressure of liquids and gases. A few years before the official discoveries, he verbally (and vaguely) formulated Gay-Lussac's and/or Charles's law about the expansion of liquids.
In 1801, he stated his Dalton's law: partial pressures of individual gases should be added to get the total result. Note that this law, one that can be given experimental evidence, strongly suggests that the different gases may "overlap" i.e. they should occupy different parts of the volume. That is already a strong hint of the atomic theory.
More importantly, he formulated the law of multiple proportions: when chemical elements combine, the ratios of their "amounts" are given by rational numbers with small numerators and denominators. We have CO and CO2 but not CO1.8. The "amounts" must be measured in moles: however, the actual term "mole" was only introduced in 1893, almost a century later.
For each compound, one mole corresponds to a different mass so we must choose different units in which the "amounts" are integer-valued. (But if you evaporate them, one "mole" always corresponds to the same volume under the same pressure and temperature. I don't quite understand whether Dalton was aware of this correct normalization: probably not.)
At any rate, in some proper units, the mixing ratios are rational. This strongly suggests a discrete underlying structure: atoms. He was not the first one to talk about this concept: Democritus and Lucretius did it millenia ago. But Dalton's picture was somewhat more modern. He also introduced a terminology for molecules that wasn't quite modern: the compounds with 2,3,4 atoms were called binary, ternary, quaternary compounds: see his picture of a new system of chemical philosophy.
He understood the following points properly:
- Elements are made out of atoms
- All atoms in the same element are identical
- For different elements, the atoms are different and have different atomic weights
- Atoms can combine to create compounds which have fixed rational ratios of the number of atoms
- Atoms can't be created or destroyed: chemical reactions only regroup them
- When atoms only combine in one ratio, it must be binary (1:1)
Of course, Dalton neglected nuclear physics in his principles: atoms of the same element may differ by the number of neutrons (isotopes) and other reactions, nuclear reactions, can also change the identity of the atoms. But we shouldn't ask for too much from a thinker in 1800.
Testability
I want to add some comments about the testability of ideas and the time-dependence of the amount and character of evidence in favor of the atomic theory. In the ancient Greece, comments about atoms were pure philosophy that was scientifically as good (or bad) as other conceivable philosophies.
But during Dalton's life, things were already very different. The law of partial pressures and especially the rational mixing ratios were extremely powerful weapons that could falsify or at least strongly disfavor many specific enough models that contradicted the existence of atoms. These laws surely didn't tell us everything we wanted to know about the structure of matter: however, they certainly told us something - a lot, in fact - and only scientific dilletantes could think otherwise.
Once the moles were introduced, people could verify new consistency checks about the atoms. Finally, the scientific enemies of the atoms evaporated in 1905 when Einstein correctly explained the Brownian motion (in work also independently pursued by Marian Smoluchowski in 1906). The alternative theories that would explain the chaotic motion of particles in liquids had to be extremely contrived, especially if they wanted to achieve the "distance goes like square root of time" power law for the random walk.
It had to be a random walk and its typical constants were pretty much universal so they had to prove some discrete collisions of basic and rather universal building blocks of all materials: the atoms and molecules. The coefficients told us something about the size of the atoms, too. All these things occurred long before we could actually "see" atoms just a few decades ago. The people who say that they must first see quarks or strings before they take the theory seriously don't tell us anything valuable about science: the only thing these people reveal is that they're narrow-minded, uncreative, slow idiots.
Baron Loránd Eötvös de Vásárosnamény: 165th birthday
Baron Loránd von Eötvös was born in Buda into an aristocratic family connected with Vásárosnamény, Hungary - a town near Ukraine - 165 years ago, on July 27th, 1848. Fortunately, Lóránd wrote both in Hungarian and German which is why most of the world can learn about his results (and forget about his full Hungarian name, Vásárosnaményi Báro Eötvös Lóránd). He focused on surface tension of liquids and gravity.
His father József was a statesman, educator, and novelist who was also a friend with Franz Liszt, the composer. When Lóránd was born, his father was a minister in the 1848 revolutionary government for a while. Gusztáv Keleti, a painter, was chosen as Lóránd's tutor, and the young future physicist turned out to be real good in drawing (especially on his trips) and poetry. Later, he became one of Europe's best mountaineers (and took a lot of photographs on his trips). He has also climbed a few peaks in the Dolomites so that one of them (in the middle of the picture below) is even named after him!
He wasn't bad. But let's return to his youth.
He studied many subjects at school. His interest in maths and physics clashed with the family tradition. So he entered the University of Pest in 1865 to study the law and become a politician. (The city was merged with Buda into Budapest in 1872.) Lóránd was taking private math lessons from Otto Petzval. His father accepted that it was science, not the law, that his son should pursue.
Lóránd worked in a chemistry lab before he moved to Heidelberg in 1867 (under Kirchhoff who taught him to make accurate measurements and Helmholtz who showed him the power of personal discussions - and others) where police cautioned him just because he was loudly singing on the street with his friends! :-)
Incidentally, the current students of the Eötvös Loránd University clearly follow his example.
After some time in Königsberg (where Franz Neumann taught him a lot about potentials and theoretical physics in general), he received a PhD in Heidelberg in 1870 (the thesis was about Fizeau's problems, one of the early steps that helped special relativity).
Once his dad died in 1871, he returned to Hungary and inherited the dad's title and a chair in the upper house of the Hungarian Parliament in 1872. In politics, he would later do some things related to education and research - for example, he founded the Mathematical and Physical Society, later named after him. But let's return to 1871. Lóránd instantly became a privatdozent of theoretical physics and added experimental physics a few years later. He married Gizella Horváth, a politician's daughter and a skillful pianist with a cool handwriting who spoke French well. Their daughters - see/click the picture on the left - became celebrities as athletes.
He returned to the problem of surface tension (from his student years in Königsberg) in 1876 and spent a decade with it. He measured it accurately and showed that its temperature dependence is universal for all liquids (Eötvös rule):\[{\rm SurfaceTension} \times {\rm MolarVolume}^{2/3} =\\
= {\rm EötvösConst} \times ({\rm TemperatureCritical} - {\rm Temperature})
\] In 1886, he fully focused on gravity which was his big scientific topic until the end of his life in 1919. And of course, he is most famous for his experiments that I will discuss in the rest of this text:
Torsion balance experiments
How did he begin to study this problem? Well, the University of Göttingen offered a prize for someone who would improve the experiments initiated by Galileo that show that the acceleration in the gravitational field is universal for all materials. And Lóránd was the right one to recycle and update the design of Henry Cavendish's experiment from the late 18th century and to improve the accuracy behind the weak equivalence principle to 5 parts per billion, much better than what Newton and Bessel have achieved previously.
In the Eötvös experiment, two different masses are attached to the ends of a horizontal rod, hung from a thin string. The rotation of the rod is monitored by looking at a mirror attached to the rod (or string) through a telescope.
If the inertial and gravitational masses were different, the Earth's gravitational acceleration (proportional to the gravitational masses) would act on the masses differently than the centrifugal "radius times omega squared" force from the Earth's spin (proportional to the inertial masses). I assume that I can afford a simple jargon because you know how to calculate these things and I don't have to introduce more accurate concepts such as the "centripetal force". This mismatch would make the rod rotate which could be seen pretty well through the telescope.
Of course no mismatch of this sort has ever been measured - even though the experimenters in the 21st century such as those in the Eot-Wash group in the Washington state are almost 1 million times more accurate than their old Hungarian colleagues.
Consequences
The weak equivalence principle demonstrated by this experiment is, of course, one of the key principles behind the general theory of relativity. General relativity satisfies this principle: it was, in fact, historically constructed by Einstein who assumed this principle once he appreciated its strength. Newton's theory agreed with this principle by choice. However, unlike general relativity, it didn't explain the principle because one could have written down a similar theory where the masses are different.
This old-fashioned, classical principle is a huge problem for all speculative physicists who try to invent a theory of "emergent" gravity where the gravitational force results from something else than the curvature of space and time - such as new kinds of superconductivity. If you can't find a reason why the description of gravity at long distances in your theory is going to be exactly equivalent to the curved spacetime as envisioned by general relativity, it is pretty much guaranteed that your theory doesn't satisfy the principle exactly.
The probability that your theory satisfies the principle approximately and it is compatible with the experimental bounds on the violation of the principle is equal to \(10^{-16}\) or less, a number related to the accuracy of the experimental tests of the equivalence principle. If there's no good reason for the double ratio of inertial and gravitational masses of protons and neutrons to be equal to one, a generic theory is going to predict this double ratio to be a "random number different from one". And the probability that such a random number differs from one by less than \(10^{-16}\) is comparable to \(10^{-16}\). Different materials, with different proportions of protons and neutrons, will respond differently and twist the torsion gadget.
In other words, people like Robert Laughlin are pretty much screwed.
How does it work in string theory? In perturbative string theory, you may derive gravity through the interactions caused by the exchange of gravitons which are closed strings in a particular vibrational state. At the beginning, you don't see any equivalence principle over here and you might be afraid that string theory is going to follow the fate of Laughlin's or Smolin's theories of gravity and go glub, glub, glub to the bottom of the sea before they even get a chance to put them out there. ;-)
However, when you study the theory more carefully, you will be able to prove that the presence of an additional graviton - a particular closed string - in any particular scattering process has an indistinguishable physical impact from a modification of the background geometry where all the strings propagate: see
Why string theory includes gravityMore precisely, the amplitudes in the original - e.g. flat - space including additional gravitons are equal to the derivatives of the amplitudes without the graviton in a general curved space, differentiated with respect to the curvature and evaluated at the original geometry. The amplitudes of particles not including gravitons at arbitrary curved backgrounds are the generating functionals for all amplitudes at a chosen background with an arbitrary number of gravitons. These words are probably useless if you don't know the formulae, anyway.
At any rate, the equivalence principle is exactly satisfied by string theory even though some descriptions of string theory are able to obscure the reasons and make the principle look like a miracle to a physicist who hasn't studied physics of the theory intensely enough. But if the reasons behind a feature of a theory are obscured, it is just the theorist's potential problem or a complication: it is not a problem of the theory itself. What matters for the fate of a theory is whether its propositions are true, as checked by observations, not whether they are easy to see. And for string theory, it is the case: its predictions related to the equivalence principle are right.
Matrix theory and AdS/CFT obscure the reasons, too. These two approaches don't even allow you to start with a general curved background, at least not in a simple way. Also, you can see the physical polarizations of the gravitons only: the pure gauge polarizations are absent from scratch. However, one can still prove that all the general facts about gravity that normally follow from general relativity are exactly satisfied because these theories - e.g. Matrix theory and AdS/CFT - can be shown to be exactly equivalent to other descriptions where the equivalence principle is manifest.
So if a theory has any chance to describe gravity as we know it today, the metric tensor must be demonstrably present in its low-energy limit and it must be possible to see that other kinds of matter depend on this metric tensor in the same way as they depend in general relativity. Because the metric tensor without anything else can't lead to finite amplitudes at higher energies, we also need some additional players in the story.
The physical phenomena and backgrounds connected in the rich network that we continue to call string theory are the only mathematically possible quantum solutions to the combined problem of finiteness and equivalence principle. It's the only framework where the curved geometry is sufficiently emergent to tame the infinities and to tell us about the inner nature of the force but also sufficiently manifest to agree with the equivalence principle as tested by the experiments initiated by this Hungarian nobleman.
And that's the memo.
John Dalton: an anniversary
Reviewed by DAL
on
July 26, 2013
Rating:
Reviewed by DAL
on
July 26, 2013
Rating:
No comments: